I’ve always had a fascination with chess, and indeed I played and won trophies for it in school. Long gone are my glory days, however, and I haven’t played regularly for going on 12 years now.
I grew up playing Chessmaster, and always wondered how it worked. When I did my AI course at uni, the curtain was pulled back a little as I learned about search algorithms, but I put this particular problem to the back of my head until I was bored after work last week.
I began scouring the web and ended up finding the Chess Programming Wiki, which has a handy getting started list. This list suggested starting with a board representation, I immediately jumped to goland and started implementing some structs. I got a little way through before going to github to make sure I was on the right track, finding a number repos mentioning something called a bitboard. My curiosity was piqued, and I started down a rabbit hole look for an answer as to why so many people did it this way.
What are they
Bit boards are a way of representing a board state with a series of composable bit masks.
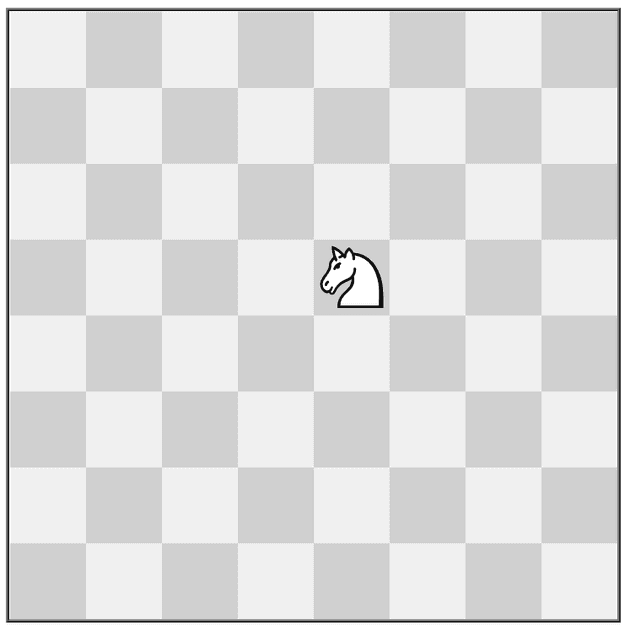
The chess board has 64 squares, so we can use a series of 64bit integers to efficiently represent and query the state of the board with bitwise operations. Consider the following board
We can represent this in binary as such
0000000000000000000000000000100000000000000000000000000000000000Or, if you prefer pictures
We can also create another mask to show where the knight can move
0000000000010100001000100000000000100010000101000000000000000000Or
We can extend this idea to efficiently query ranks, files, piece attacks etc. It’s actually ingenious, since we can do bitwise operations to combine the masks. For example, “All squares on the G file where the knight can move” is a bitwise AND opration between the G file and the knight’s possible moves, which gives us
0000000000000000000000100000000000000010000000000000000000000000It’s a very elegant, if verbose solution. I’ve since learned it’s easier to pre calculate the squares a piece can move to, storing them in hashmaps of 64 bit integers keyed to the squares. Since there’s only 6 different pieces with 64 possible positions, it becomes trivial and fast to just have a constant value to query in the code. Needless to say I’m blown away by this data structure.
Why this eluded me
My marveling at such a simple data structure aside, it caused me to reflect on why I didn’t think of something like this. I know a long int is 64 bits, I know about bitmasks, I should have been able to put this together. I think the main reason is because I’ve spent so long in the OO paradigm that it’s very difficult for me to break those abstractions.
The bitboard exposed a giant hole in my own thought processes, and certainly for performance’s sake in future I will definitely give more thought to how I can exploit masks and primitive types like this. I’m very glad I decided to finally learn how to make a computer play chess.